O gomoku e os jogos m,n,k

Continuando na senda dos jogos abstractos de tabuleiro, o Gomoku é um jogo originário do Japão, tradicionalmente jogado num tabuleiro de Go 19x19 com as peças deste mesmo jogo. Dois jogadores alternam na colocação de peças brancas e pretas no tabuleiro, tendo o objectivo de colocar cinco peças em linha (que pode ser ao longo de uma linha, coluna ou diagonal). As regras não podiam, portanto, ser mais simples. É o jogador com as peças pretas que começa a jogar, ao contrário do xadrez ou de outros jogos tradicionais de tabuleiro.

Quando é jogado num tabuleiro 15x15, recebe o nome de Renju (imagem abaixo).



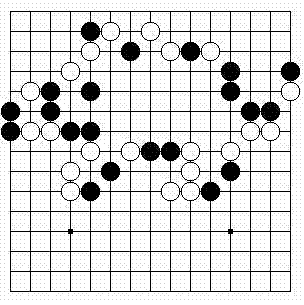
Foi provado por Victor Allis (através de uma pesquisa por computador) que o jogo termina sempre numa vitória para as pretas se estas usarem uma estratégia perfeita. Mesmo em tabuleiros de diferentes tamanhos, é bastante claro que as pretas têm vantagem e, como tal, existem diversas variantes deste jogo em que foram criadas algumas regras adicionais para nivelar o jogo.

Se generalizarmos o jogo para um tabuleiro m x n, em que um jogador para ganhar tem de fazer k peças numa linha, obtemos os jogos (m,n,k), que são de grande interesse do ponto de vista matemático, mas como é óbvio só alguns são jogados na prática. Por exemplo, o jogo (3,3,3) é o tão conhecido jogo do galo.

É interessante ver como, neste caso, com um argumento simples é possível provar que o jogador que joga em 1º caso tem pelo menos garantido o empate (pode ter garantida a vitória, dependendo do jogo, mas este argumento prova que ele, pelo menos, não perde). Imagine-se que o 2º jogador tem uma estratégia E que lhe permite ganhar (onde aqui uma estratégia não é mais do que uma árvore que a cada lance possível do adversário permite responder com um lance que continua a permitir o 2º jogador forçar a vitória na posição resultante). Então, o 1º jogador faz a primeira jogada ao acaso e depois limita-se a copiar a estratégia do seu adversário nos restantes lances. Se em algum ramo da árvore se vir forçado a jogar para uma casa em que já jogou (porque joga aleatoriamente na 1ª jogada) limita-se a jogar aleatoriamente de novo. Ou seja, o segundo jogador também tem garantida a vitória. Ora, isto é impossível porque não pode haver dois adversários a ganharem um mesmo jogo.

À primeira vista, o leitor seria levado a pensar que este argumento se aplica a quaisquer jogos simétricos (em que ambas as partes têm disponíveis os mesmos movimentos) e, portanto, ao xadrez. Contudo, existe um pormenor subtil que invalida a aplicação deste raciocínio. Nos jogos (m,n,k) não há nenhuma desvantagem que se possa imaginar de fazer o primeiro lance ao acaso - uma configuração do tabuleiro em que tenho n peças + 1 colocada ao acaso é sempre pelo menos tão boa como aquela em que tenho n peças nas mesmas posições - mas no xadrez, um lance ao acaso como por exemplo 1. Ca3 pode enfraquecer a posição branca, pelo que este argumento não se aplica ao xadrez, damas, e outros jogos de tabuleiro tradicionais.